二分ヒープ

二分ヒープ(にぶんヒープ,バイナリヒープ,Binary heap)とは、二分木を使って作られるヒープ(データ構造)の特に単純な種類のひとつである。それは、二分木に、以下の2つの制約を追加したものとみなせる。
- 要素間の順序関係に従った比較によって、各々のノードはそのノードの子よりも大きいか等しくなるように配置される(heap property)
- 木は完全にバランスの取れた二分木(すべての葉は同じ高さにある)になるか、木のもっとも高い方がすべて埋まっていないならば、ノードは左から右へ順に埋まっていく(shape property)
ここで「より大きい」とは、比較のためにいかなる比較関数を選択するかによって意味づけられる。ノード内のデータが常に数値であるとは限らないので、数量的な『より大きい』である必要はなく、数理的に言うところの全順序であればよい。
また、heap propertyのような制約を持つ木を一般に「部分順序付き木」と言う。ヒープは、部分順序付き二分木に、さらにshape propertyの制約を加えたものである。配列を使って実装できるという特性がある(後述)。
比較が数量的な「より大きい」であるヒープは最大ヒープ (max heap) と呼ばれる。また、比較が数量的な「より小さい」であるヒープは最小ヒープ (min heap) と呼ばれる。たとえば優先順位付き待ち行列において、小さい値が高い優先度を意味するのであれば、最小ヒープを使う。
ヒープ内の子同士の順序は、heap propertyによって特定できないことに注意すること。つまり、親を同じくする二つの子は、制約を壊さない限り自由に入れ替えることができる(Treapと比較せよ)。
ヒープ操作[編集]
ヒープへの追加[編集]
すでに存在しているヒープに、前述の制約を保ったまま要素を追加するには、up-heap(bubble-up, percolate-up, sift-up, trickle-up, heapify-up, cascade-up 等とも)と呼ばれる操作によらなければならない。以下のアルゴリズムにしたがって、二分ヒープに対し O(log n) で操作を行うことができる。
- ヒープの最下層に要素を追加する
- 追加した要素とその親を比較する。正しい順序で並んでいるならば、停止する。
- もし順序が正しくないならば、親と追加要素を交換して、2に戻る。
この操作は、木上で最大各々の深さで行う必要がある。つまり、木の高さ分行う必要があるので、O(log n) かかる。しかしながら、およそ要素の50%が葉であり最下層から2レベルまでには75%の要素が含まれることから、新しい要素を挿入する際、ヒープを維持するために、上向きに2, 3レベル動かすくらいですむだろう。このように、二分ヒープは、要素の挿入には平均 O(1) の固定時間をサポートする。
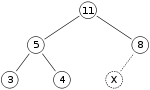
最大ヒープと呼ばれるのは以下のようなものである。
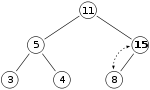
ここで、ヒープに「15」という数字を付け加えたい。まず最初に X の印がついている場所に「15」を置く。しかし、「15」は親である「8」より大きいのでヒープの制約条件に違反している。そこで、「15」と「8」を入れ替える。最初の入れ替え後、ヒープは以下の様になる。
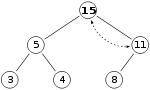
しかし「15」はその親である「11」よりも大きいので、まだヒープの制約条件に違反している。そこで、再度入れ替える必要がある。
これで、適切な最大ヒープができた。
ヒープからルートの削除[編集]
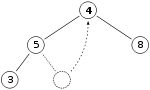
ヒープからルートを削除する手順、つまり効果的に最大ヒープ内で最大要素を検索したり最小ヒープから最小要素を検索する手順は、up-heap とよく似ている。これを down-heap (bubble-down, percolate-down, sift-down, trickle down, heapify-down, cascade-down) と呼ぶ。ルートを削除するということは、ルートを木の末端の要素と入れ替えることである。前と同じ最大ヒープを例にとると、
「11」を削除して「4」と入れ替える。
親である「4」は子である「8」よりも小さいのでヒープの制約条件に違反している。この2つの要素を交換すればヒープの制約条件は保たれ(「4」はより大きい子と交換される。最小ヒープならばより小さい子と交換される)、これ以上操作の必要はない。
ヒープからルート以外の削除[編集]
木構造を配列で管理している場合は、ノード → 配列番地への管理が別途必要である。これは連想配列でもできるし、ノードに持たせても良いし、現れるノードが決まっているのなら普通の配列でも管理できる。
その上で手順は以下の通り。
- 削除したのが木の末端のノード(配列管理なら配列の末尾)なら詰める必要が無いので終了。
- 木の末端のノードを抜けた場所へ持ってきて、down-heap する。
- もし、上記の操作で木が変化しないならば、up-heap する。
値の更新[編集]
値の更新は例えばダイクストラ法やA*などで使用する。最大ヒープの場合、ノードの値を更新した後、値が増えるなら up-heap し、値が減るなら down-heap すれば良い。計算量は増えるが、削除して追加でも実装可能。
計算量[編集]
| 操作 | 最悪計算量 | 平均計算量 |
|---|---|---|
| 最大値の取得 | O(1) | O(1) |
| 要素数の取得 | O(1) | O(1) |
| 追加 | O(log n) | O(1) |
| 削除 | O(log n) | O(log n) |
| 値の更新 | O(log n) | O(1) |
平均計算量だけでなく、最悪計算量も O(1) にしたい場合は、他のヒープ構造を検討するべきだが、二分ヒープを配列で実装した場合、計算量の定数項分が、一般的に他のアルゴリズムよりも小さく、現実的には二分ヒープが最速である場合も多く、libstdc++ (gcc) の priority_queue の実装ではプリミティブ型の場合は二分ヒープの使用を薦めている[1]。フィボナッチヒープを使った場合、平均計算量ではなく償却計算量で、追加・更新が O(1)、削除が O(log n) になる。
ヒープの実装[編集]
古典的な二分木データ構造を使って、二分ヒープ木を構築することは完全に可能である。ただ、要素を追加する時に、次に追加する要素をぶら下げるべき要素を探すのに手間がかかる、という問題がある。素直に実装した二分木では、根元に向かうリンクが存在しないためである。これは「スレッド木」と呼ばれているデータ構造により困難を緩和できる。
スレッド木とは、末端の要素において、子要素への参照として null 等を格納するかわりに、通りがけ順(二分木#行きがけ順、通りがけ順、帰りがけ順探索を参照)における先行要素と後続要素への参照を格納し、探索を容易にした二分木データ構造である。
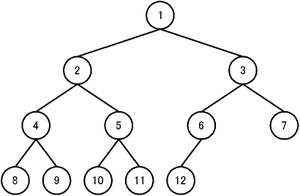
しかし、より普及しているやり方は、配列に写す方法である。以下のように、ほとんど完全な二分木の要素に番号を付けてみる。まず、根元の要素に 1 という番号を付ける。以下幅優先で順番に番号を振ってゆく(図を参照)。
すると、番号に次のような規則があることがわかる。ある要素に振られた番号を n とすると、
- 左の子は 2n
- 右の子は 2n + 1
- 親は floor(n / 2) (※多くの処理系で、整数除算として単に n / 2 で実装できる)
- 兄弟(ないし同世代) n + 1, n - 1
この規則性により、ほとんど完全な二分木は、ポインタ用のメモリを必要とせず、(可変長の)配列に、たいへん効率よく詰め込むことができ、また要素を辿ることもできる[2]。これは暗黙のデータ構造の一つの単純な例である。
このやり方は、ヒープソートで特に役に立つ。入力の配列を、ヒープを格納するために再利用し、in-place なソートが実現できるからである。
0 からの番号付けだと、式が少し複雑になるので、1 からの番号付けが一般に使われる。C言語など、配列が 0 始まりの場合には、配列の 0 番目を、「ルートのルート」と言われるような手法のための番兵のデータを置いたり、そのヒープ木の現在の要素数の格納などに流用することがある。 二分ヒープ木のマージは、等しいサイズのヒープ2個の場合、Θ(n)だけかかる。マージ処理がよく使われる処理であるならば、二項ヒープのような違うヒープ実装を推奨する。
注[編集]
- ^ Priority-Queue Design
- ^ さらに深い考察が「ヒープの正体」(たなかともひさ)にある